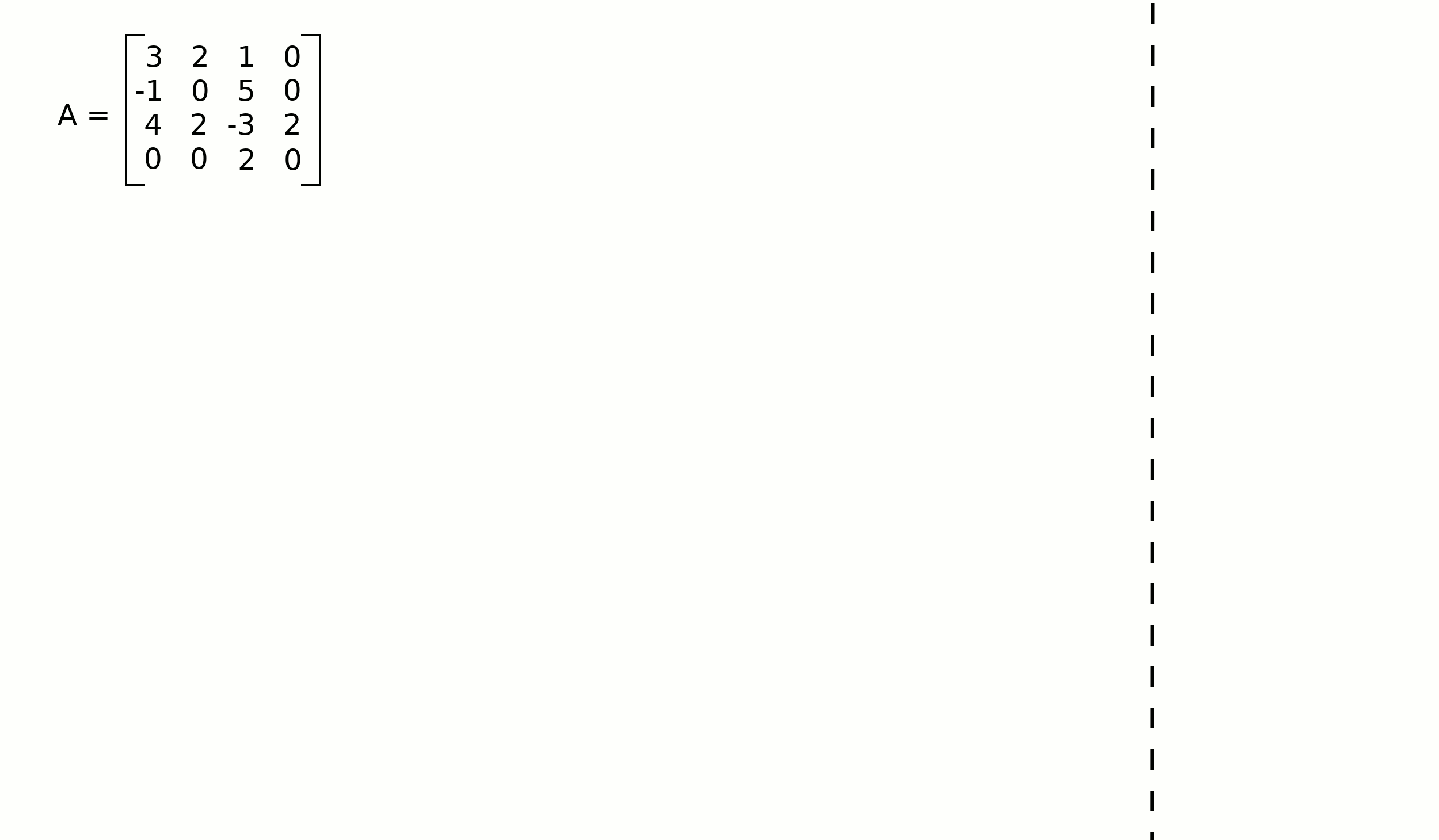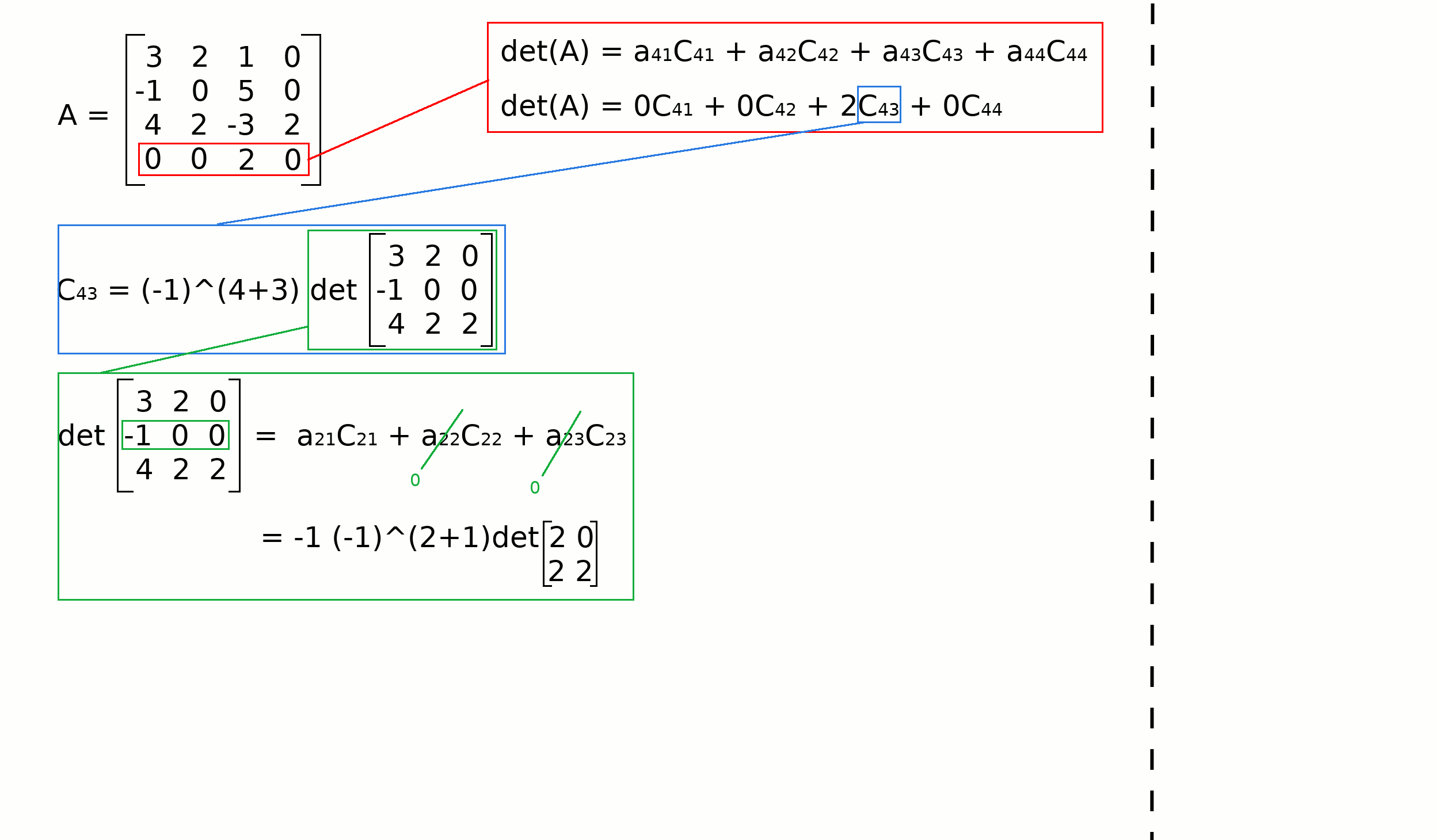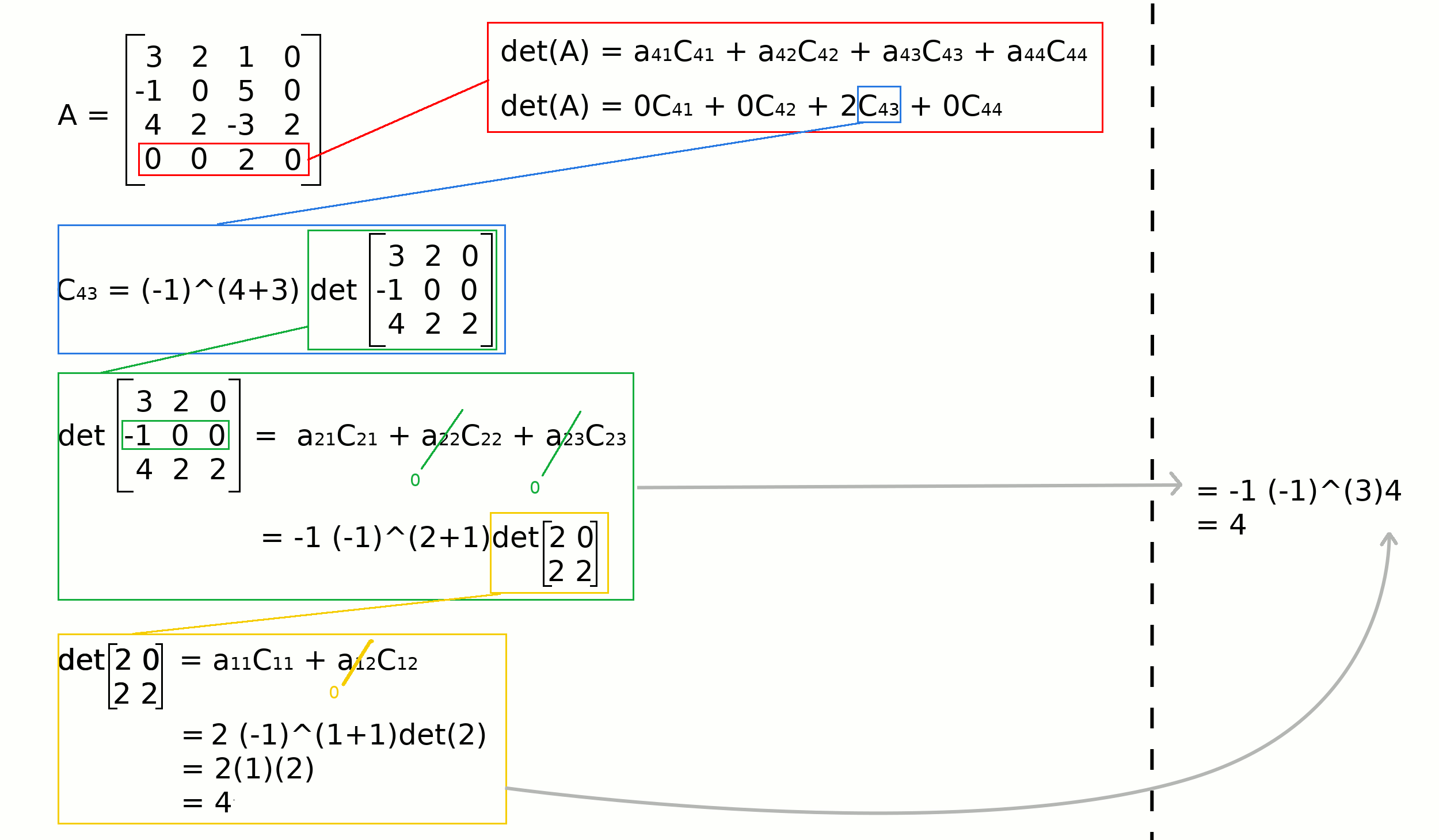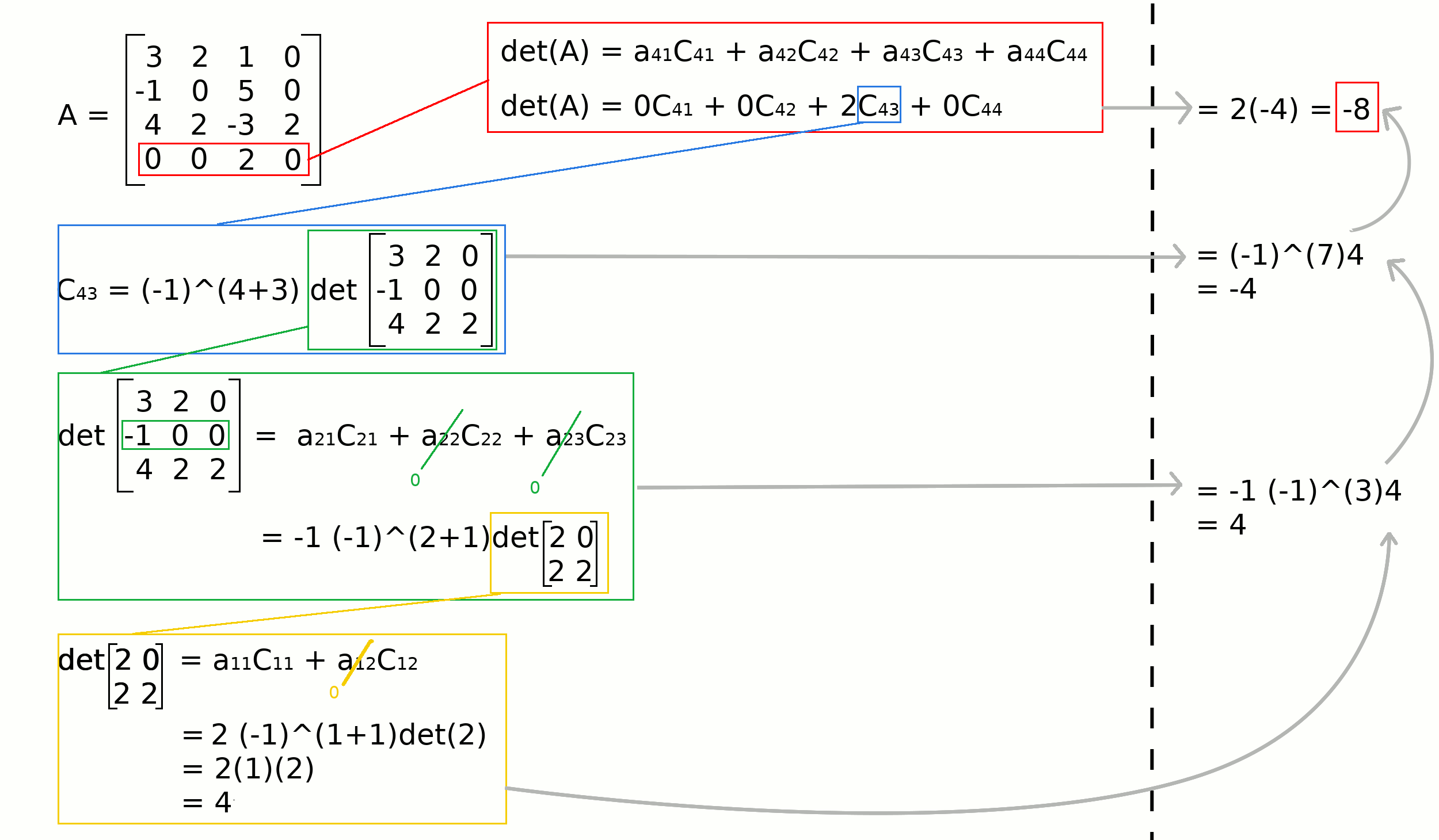Matrix Determinant 🟠#

Write functions that return the determinant of square matrix of orders (\(2\times2\)), (\(3\times3\)), and (\(n\times n\)).

Rules#

  1. Function returns a integer.

  2. You must not use any external function to calculate the determinant.

Determinant overview#

Order (\(2\times2\))#

In the case of a (\(2\times2\)) matrix the determinant can be defined as

\[\begin{split} \text{det}(A) = \text{det} \left( \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \right) = a_{11}a_{22} - a_{12}a_{21}\end{split}\]

Larger Orders#

Minor of Matrix#

Minor of matrix for a particular element in the matrix is defined as the matrix obtained after deleting the row and column of the matrix in which that particular element lies.

- cuemath

Note

See the Minor of Matrix challenge for more details.

Cofactor of Matrix#

The \((i,j)\) cofactor \(C_{ij}\) is defined in terms of the minor \(M_{i,j}\) by

\[ C_{ij} = (-1)^{i+j}\text{det}(M_{ij}) \]

Determinant using cofactor expansion along the \(i^{\text{th}}\) row#

For a Matrix \(A\) like:

\[\begin{split} A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} \end{split}\]

You can use one arbitrary row and the cofactor expansion to get the determinant of \(A\):

\[ \text{det}(A) = \sum_{j=1}^{n} a_{ij}C_{ij} \]

For example, if you chose the first row, the determinant is:

\[ \text{det}(A) = a_{11}C_{11} + a_{12}C_{12} + a_{13}C_{13} \]

Note

You can use any row you want.

Recursive formula#

A recursive formula must have a starting point. For cofactor expansions, the starting point is the case of \(1 \times 1\) matrices.

- Dan Margalit, Joseph Rabinoff

Consider a \(1 \times 1\) matrix \(A\) like:

\[ A = \begin{bmatrix} a_{11} \end{bmatrix} \]

Then, the determinant of \(A\) is:

\[ \text{det}(A) = a_{11} \]

Therefore, to determine the determinant of any square matrix, you can recursively apply the cofactor expansion up to the point that all matrix have a \(1 \times 1\) dimension.

Example#

cofactor