Solution: Minor of Matrix
Contents
Solution: Minor of Matrix#
Write a function that returns the Minor of Matrix of a 3x3 Matrix for a given line \((i)\) and column \((j)\)
Rules#
Function returns a Numpy ndarray of shape=2x2
Function should work for all possible \(i,j\) combination
Solution#
We are going to explore two solution types
Using
numpy.delete: this function deletes entire rows or columnsUsing advanced indexation and
numpy broadcasting
The solution using the delete function is quite straightforward and simple, however, learning how to use advanced indexing and broadcasting can be very useful, so if you can, take the time to analyse this type of solution.
Using numpy.delete#
import numpy as np
A = np.array([[ 9, 12, 18],
[ 2, -2, 5],
[11,-17, 19]]
)
def get_minor_ij(A, i, j):
A = np.delete(A, i-1, axis=0) # remove a row (axis=0)
A = np.delete(A, j-1, axis=1) # remove a column (axis=1)
return A
get_minor_ij(A, 1, 2)
array([[ 2, 5],
[11, 19]])
Using Advanced Indexation#
Wrong solution#
I know it seems a little weird that I come up with a wrong solution, but as I believe this is a pretty common mistake, I’ll present it and then discuss solutions.
def get_minor_ij(A, i, j):
# create line and column lists
line = [0, 1, 2]
column = [0, 1, 2]
# remove (i,j) from lists
line.remove(i-1)
column.remove(j-1)
return A[line, column]
As we are working with 3x3 matrix, I create lists for the index columns and then I removed the (i,j) from it. Finally I returned the minor matrix using the index lists.
Did you came up with a similar solution?
So, lets see what is wrong:
get_minor_ij(A, 1, 2)
array([ 2, 19])
We were expecting the following result:
But the solution gave us just two elements from the minor matrix main diagonal.
Lets look the index lists:
line = [1, 2]
column = [0, 2]
Our result is referent to the elements in position (1, 0) and (2, 2), but we are missing the cross product elements, that is, the elements in position (1, 2) and (2, 0).
One solution would be to write index lists that include the cross product, which in this case would be:
line = [[1, 1], [2, 2]]
column = [[0, 2], [0, 2]]
This solution has some difficulties. First it is necessary to place the indexes in the correct order, second it is necessary to use the correct dimension. In this case the solution is a 2x2 matrix, so the indexing must be consistent. If you want to try
this kind of solution, maybe numpy.indices may help. See more here.
Broadcasting overview#
The broadcast concept is quite extensive and can be difficult to understand, but don’t worry as it has many very simple applications.
If you want to know more about it, please see the NumPy documentation here
The main idea about Broadcasting is to “stretch” the operation across different shaped arrays. Lets see a basic example:
a = np.array([1, 2, 3])
b = 2
a * b
array([2, 4, 6])
Even though b does not have the same dimension as a, NumPy understands that the operation must be applied on each element of the a array.
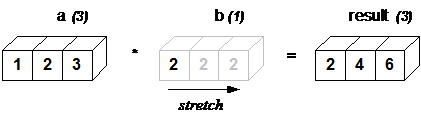
Now, look what happens if we perform some operation between two arrays:
a = np.array([[ 0],
[10],
[20],
[30]]
)
b = np.array([1, 2, 3])
a*b
array([[ 0, 0, 0],
[10, 20, 30],
[20, 40, 60],
[30, 60, 90]])
Again, b does not have the same dimension as a, but NumPy is able to perform
the operation by stretching boot a and b arrays to same dimension.
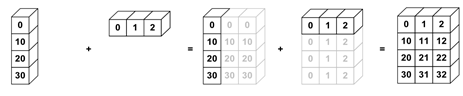
See a very similar example. This time the broadcasting is going to fail:
a = np.array([0, 10, 20, 30])
b = np.array([1, 2, 3])
a*b
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
/tmp/ipykernel_1938/4060636190.py in <module>
1 a = np.array([0, 10, 20, 30])
2 b = np.array([1, 2, 3])
----> 3 a*b
ValueError: operands could not be broadcast together with shapes (4,) (3,)
This happens because the array dimensions are not compatible for broadcasting.
In the first scenario we had the shapes: (4, 1) + (1, 3). The broadcast stretch the arrays to (4, 3) + (4, 3).
But in the second scenario, the shapes were (4) and (3) –> not compatible.
Are you confused? Let’s go back to our challenge and see how we can apply this knowledge
Broadcasting Solution#
This solution is almost equal to before, the only difference is that the line
index list has a different shape (3 x 1).
Now the dimension of line and column are not equal, so NumPy will try to
stretch the lists and the result will be a 2x2 matrix, ie., the solution will
automatically include the crossed terms and arrange them in the correct
dimensions!
def get_minor_ij(A, i, j):
# create line and column lists
line = [[0], [1], [2]] # shape (3x1)
column = [0, 1, 2] # shape (1x3)
# remove (i,j) from lists
line.remove([i-1]) # add []
column.remove(j-1)
return A[line, column]
get_minor_ij(A, 1, 2)
array([[ 2, 5],
[11, 19]])
Generalizing the solution#
If you want to create a function that works for dimensions larger then 3, you
can create line and column based in the shape of A and then reshape the
line for a (nx1) array.
def get_minor_ij(A, i, j):
# create line and column lists
line = list(range(A.shape[0])) # shape (1x3)
column = list(range(A.shape[1])) # shape (1x3)
# remove (i,j) from lists
line.remove(i-1)
column.remove(j-1)
# reshape line
line = np.array(line).reshape(len(line),1)
return A[line, column]
get_minor_ij(A, 1, 2)
array([[ 2, 5],
[11, 19]])
Once you understand the broadcast process, you can go for fancy solutions.
Here I will suggest the NumPy ix_ function that reshapes the index
list to fit with broadcasting. It is basic our first solution, but with a
different reshape approach:
def get_minor_ij(A, i, j):
# create line and column lists
line = [0, 1, 2] # shape (1x3)
column = [0, 1, 2] # shape (1x3)
# remove (i,j) from lists
line.remove(i-1) # add []
column.remove(j-1)
return A[np.ix_(line, column)] # change the line shape here!
get_minor_ij(A, 1, 2)
array([[ 2, 5],
[11, 19]])
See how ix_ reshapes line:
line = [0, 1, 2] # shape (1x3)
column = [0, 1, 2] # shape (1x3)
print (line, column)
print (np.ix_(line, column))
[0, 1, 2] [0, 1, 2]
(array([[0],
[1],
[2]]), array([[0, 1, 2]]))
Testing#
Check if your function returns the expected value using the cell below.
import unittest
class UnitTests(unittest.TestCase):
def setUp(self):
self.A = np.array([[ -7, 4, -2],
[ 2, -3, 5],
[-18, 10, 0]]
)
def test_type(self):
self.assertTrue(isinstance(get_minor_ij(A, 1, 2), np.ndarray), 'The function should return a NumPy array')
def test_shape(self):
self.assertTrue(get_minor_ij(self.A, 1, 2).shape == (2, 2), "The function should return an 2x2 array")
def test_minor11(self):
self.assertEqual(get_minor_ij(self.A, 1, 1).tolist(), [[-3, 5], [10,0]])
def test_minor12(self):
self.assertEqual(get_minor_ij(self.A, 1, 2).tolist(), [[2,5], [-18,0]])
def test_minor13(self):
self.assertEqual(get_minor_ij(self.A, 1, 3).tolist(), [[2,-3],[-18,10]])
def test_minor21(self):
self.assertEqual(get_minor_ij(self.A, 2, 1).tolist(), [[4,-2],[10,0]])
def test_minor22(self):
self.assertEqual(get_minor_ij(self.A, 2, 2).tolist(), [[-7,-2],[-18,0]])
def test_minor23(self):
self.assertEqual(get_minor_ij(self.A, 2, 3).tolist(), [[-7,4],[-18,10]])
def test_minor31(self):
self.assertEqual(get_minor_ij(self.A, 3, 1).tolist(), [[4,-2],[-3,5]])
def test_minor32(self):
self.assertEqual(get_minor_ij(self.A, 3, 2).tolist(), [[-7,-2],[2, 5]])
def test_minor33(self):
self.assertEqual(get_minor_ij(self.A, 3, 3).tolist(), [[-7,4],[2,-3]])
unittest.main(argv=[''], verbosity=2,exit=False)
test_minor11 (__main__.UnitTests) ... ok
test_minor12 (__main__.UnitTests) ... ok
test_minor13 (__main__.UnitTests) ... ok
test_minor21 (__main__.UnitTests) ... ok
test_minor22 (__main__.UnitTests) ... ok
test_minor23 (__main__.UnitTests) ... ok
test_minor31 (__main__.UnitTests) ... ok
test_minor32 (__main__.UnitTests) ... ok
test_minor33 (__main__.UnitTests) ... ok
test_shape (__main__.UnitTests) ... ok
test_type (__main__.UnitTests) ... ok
----------------------------------------------------------------------
Ran 11 tests in 0.006s
OK
<unittest.main.TestProgram at 0x7f0132eb7df0>


